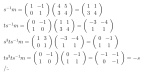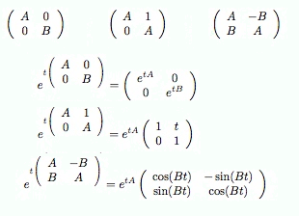2015/12/08 · 17:50

Einstein-Penrose ‘s strong sum convention


the rank one tensors’ basis changes

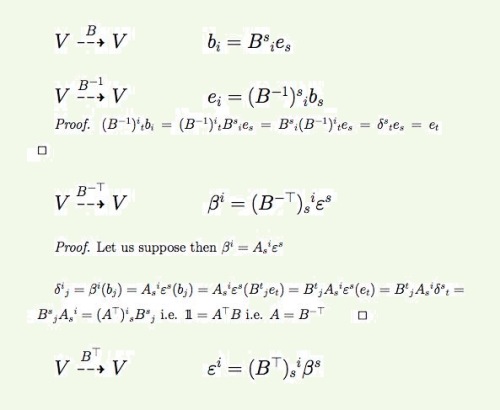
abstractrelativity017

2 Comments

Filed under math, mathematics, multilinear algebra, word algebra

Tagged as , , , , , ,

2015/10/23 · 19:33

a level surface


A level surface f^{-1}(1) for the function f(x,y,z)=x^2+y^2+z^2-3xyz
levelsurf014

3 Comments

Filed under math

2015/06/17 · 13:39

splitting into handlebodies


spleeti

Leave a comment

Filed under 3-manifold, 3-manifolds, fiber bundle, low dimensional topology

Tagged as

2015/05/22 · 14:15

short exact sequence and center


Let us prove:

Let 1\to A\stackrel{f}\to B\stackrel{g}\to B/A\to 1 be a short exact sequence, if the center Z(B/A)=1  then Z(B)<A

Proof:  When x\in Z(B) then g(x)\in Z(B/A), so g(x)=1.

Therefore x\in\ker (g)={\rm im}(f)=A

\Box

 

Leave a comment

Filed under 3-manifold, algebra, group theory, word algebra

Tagged as

2015/03/12 · 21:49

Pascal’s Rule and double induction


If S is a set with \#S=n and T\subset S such that \#T=k then there are {n\choose k} different of them.

Follow the link pascalbernoulli for a double induction proof.

Leave a comment

Filed under math

2015/02/27 · 10:00

primer parcial, examen de multi


aplicado ayer √

1erexamAlMu

1 Comment

Filed under math

2015/01/25 · 18:48

three jordan two-by-two matrices and exponential


temareas?

How many three-by-three forms are there?

: )

2 Comments

Filed under math