multilineal lección 3

from vector-calculus with differential forms in 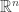$\mathbb{R}^n$ (euclidean ones) and differential forms in surfaces till tensor-fields on manifolds or differentiable section into tensor-products of the tangent-bundle of a space

vectors in r-3 (3d-space) are used in two ways as a geometric tangent objects and/or as a differential operator.

an element of r-3 is a vertical array of scalars which determine a directional derivative:

$X=X^1e_1+X^2e_2+X^3e_3$

$Xf=\langle X,{\rm{grad}}f\rangle$

$=X^1\frac{\partial f}{\partial x^1}+X^2\frac{\partial f}{\partial x^2}+X^3\frac{\partial f}{\partial x^3}$

with this simple device one can answer how much a given definite function in r-3 vary in some particular vector field and $X$ shouldn’t necessarely constant, so $Xf$ measure what quantity of variation of $f$ to the direction $X$ .

Front tim3 to time would be betta try to visualice $X$ as an operator

$X=X^1\frac{\partial }{\partial x^1}+X^2\frac{\partial }{\partial x^2}+X^3\frac{\partial }{\partial x^3}$

But we can also want to answer how another vector field $Y$ varies with respect to $X$ , this is:

$D_XY=[JY]X$

with this one is compeled to use how the components of $Y$ vary toward $X$

${\cal{X}}(\Omega)=\{\mbox{differentiable}\ X:\Omega\to{\mathbb{R}}^3\}$ : the set of smooth vector field on the open set $\Omega\subseteq\mathbb{R}^3$ . This set can be considered as a $C^0(\Omega)$ -module, that is there is an action:

$C^0(\Omega)\times{\cal{X}}(\Omega)\to{\cal{X}}(\Omega)$
.
$\Lambda^0(\mathbb{R}^3)=C^{\infty}(\mathbb{R}^3)$
.
$\Lambda^0(\Omega)=C^{\infty}(\Omega)$
.
${\mathbb{R}^3}\cong\{\frac{\partial}{\partial x},\ \frac{\partial}{\partial y},\ \frac{\partial}{\partial z}\}$
.
$\Lambda^1({\mathbb{R}^3})={\rm{gen}}\{dx, dy,dz\}$
.
$dx\wedge dy=dx\otimes dy-dy\otimes dx$
.
$\Lambda^2(\mathbb{R}^3)={\rm{gen}}\{dy\wedge dz,dz\wedge dx,dx\wedge dy\}$
$dx\wedge dy=-dy\wedge dx$
$dx\wedge dx=0$
.
$\Lambda^3(\mathbb{R}^3)={\rm{gen}}\{dx\wedge dy\wedge dz\}$

vector calculus and linear algebra were devised by Grassmann-SaintVenant-Gibbs-Heaviside the years 1820-1900 inter,

to give the tensor analysis, used by Einstein to create relativity in 1907 (approx) and Schrödinger quantica in the 1920’s

to detect the next upgrading you gonna need to go just to Heisenberg-Dirac-Cartan circa 1925-1960

the chinesse’s mathemagizian Shiing-Shen Chern around 1975 gaves us the characteristic classes which are the new basic-math tools to unlock the misteries of all maths and sciences…

Evidently, any Bachellor in a CEI (exact science institution) should, at least, be aware that science had grew too high but too systematic too

You could find many Master Science individuals asking for Lie groups and Lie algebras which had be metioned in their graduate ateliers.

To a PhD : ignorating these matters is a MEASURE of their level of culture and of intelligence i.e. competence

Picture this:

today, vector calculus and linear algebra are courses taken by a variety of CEI-students, having teachers of all kinds of culture trying to make them assimilated by their pupils

corruption (tranza-y-media), however time to time one or two (y lo logran de cuando en cuando…) Those who advance will cry mamma (os que avanzan al M.Sc. llorarán a su mamá…) the PhD’ll gonne mad (los PhD enloquecerán…)

Why do not imagine all world to know this techniques? (¿Porqué no inventar querer que todo mundo sepa qué es un algebra de grassmann de un espacio vectorial entonces…?)

S.S. Chern forecasted in brief will see how (Chern pronóstico que en breve veríamos como el concepto de fibrado vectorial y su conexión de Leví-Civita llegaría) should reach (a la escuela de ingeniería… bah), we are at least (apenas lo estamos) wittnessing (atestiwändo):

how the physic’s schools and one-or-two technical centers are getting acquainted!

: )

https://juanmarqz.wordpress.com/wp-content/uploads/2009/10/lecciontres.pdf

9 responses to “multilineal lección 3”

Pingback: lecciones de multilineal ligas « juanmarqz
David D

2010/05/15 at 00:55

ha otra cosa maestro, que es un r-simplex?, lo estoy checando donde definen el operador frontera, el ingles se me medio traba por eso no lo entiendo en totalidad

- juanmarqz
  
  2010/05/15 at 10:39
  
  es una construcción en r-dimensiones (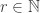 $r\in\mathbb{N}$ ) que generaliza las nociones de intervalo acotado, triangulo, tetrahedro, etc
  para después con ellos armar espacios poliédricos, estos son un poco más fáciles de estudiar que las variedades (manifolds)…
  
David D

2010/05/15 at 00:52

q onda maestro, he estado checando el libro geometry, topology and physics de M Nakahara y pues segun veo esta muy chingon, ya lo ha checado usted?, que tal lo recomienda?, viene todo el show del wedge, cohomologia etc….

- juanmarqz
  
  2010/05/15 at 10:33
  
  pude encontrar:
  
  http://www.scribd.com/doc/14600260/Geometry-Topology-and-Physics-Mnakahara
  
  y es un libro del siglo pasado 1989…
  
  en el primer capítulo dice que es para aquellos que ya saben cuántica y relatividad… eso no quiere decir que no entres y no veas las cosas que ya sabes (comparar hasta donde puedas)…
  
  Una opinión genérica que tengo es que no hay libros inútiles, pero aveces son malos y este de Nakahara, parece no serlo…
  
  Lo ultramejor es tener varios del tema y compararlos…
  
c-qit

2009/10/23 at 11:55

ejemplo $xy^2\left(y\partial_x-e^x\cos(y)\partial_y\right)=xy^3\partial_x-xy^2e^x\cos(y)\partial_y$

qit

2009/10/23 at 11:52

la $C^{\infty}(\Omega)\times{\cal{X}}(\Omega)\to{\cal{X}}(\Omega)$ esta dada por
$(f,X)\mapsto fX=(fX^s)\partial_s$

c-qit

2009/10/19 at 09:23

las ideas de hace 170 años de Grassmann se ven realizadas cuando el objetivo de explicar el de Rham para formas euclideanas conectan las principales operaciones del análisis vectorial, dejándonos los principios tensoriales elementales a nuestra merced…

c-qit

2009/10/08 at 22:37

euclidean de Rham’s complex

.

$0\to\Lambda^0\mathbb{R}^3$

$0\mapsto 0$

.

$\Lambda^0\mathbb{R}^3\to\Lambda^1\mathbb{R}^3$

$f\mapsto df=\frac{\partial f}{\partial x^s}dx^s=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz$

.

$\Lambda^1\mathbb{R}^3\to\Lambda^2\mathbb{R}^3$

$\eta\mapsto d\eta=d\eta_s\wedge dx^s$

$d\eta_s=\frac{\partial \eta_s}{\partial x^{\mu}}dx^{\mu}=\frac{\partial \eta_s}{\partial x}dx+\frac{\partial \eta_s}{\partial y}dy+\frac{\partial \eta_s}{\partial z}dz$

.

$\Lambda^2\mathbb{R}^3\to\Lambda^3\mathbb{R}^3$

$\Omega\mapsto d\Omega=d\Omega_{st}\wedge dx^s\wedge dx^t$

$d\Omega_{st}=\frac{\partial \Omega_{st}}{\partial x^{\mu}}dx^{\mu}=\frac{\partial \Omega_{st}}{\partial x}dx+\frac{\partial \Omega_{st}}{\partial y}dy+\frac{\partial \Omega_{st}}{\partial z}dz$

.

$d:\Lambda^3\mathbb{R}^3\to0$

—————————————–

.

$\Lambda^0(\Omega)=\{f:\Omega\to\mathbb{R}\}$

$\Lambda^1(\Omega)=\{f_1dx+f_2dy+f_3dz\quad,\quad f_s\in \Lambda^0(\Omega)\}$

$\Lambda^2(\Omega)=\{g_1dy\wedge dz+g_2dz\wedge dx+g_3dx\wedge dy\quad,\quad g_s\in \Lambda^0(\Omega)\}$

$\Lambda^3(\Omega)=\{fdx\wedge dy\wedge dz\quad,\quad f\in \Lambda^0(\Omega)\}$