topological bundle
A bundle is a bunch of objects:
- a topo space
which will be called the base of the bundle
- another topo space
called the total of the bundle
- a topo-space
, called the fiber of the bundle and
- a scheme of maps
such that
for each there exists
neighborhood of
in
such that the fiber
is homeomorphic to
via
in such a way that the composition
is the projection in the second factor. The map is called the projection of the bundle and any other map
that obeys
usualy is called a section of the bundle.
Examples of sections in vector bundles are the famous:
vector-bundles and/or tensor-fields on surfaces
- if
is the tangent bundle on a surface then a map
is called vector field on the surface…
other bundle are:
- ——————————————————————————–
is the cotangent bundle
is called covector field
- ————————————————————————————–
is the rank two mixed tensor bundle
is a rank two mixed tensor field
- —————————————————————————————————
is a rank three mixed tensor field 2-contravariant and 1-covariant
- ————————————————————————————————————————–
is the rank
tensor bundle n-contravariant and m-covariant
is a rank
mixed tensor field n-contravariant and m-covariant
—————————————————
the covariant derivative allow you to “connect” several bundles
on we have
… remember that if and
then
. That is
——————————————————–
and on a surface we have
——————————————————–
it is true that determines
as a rank two mixed tensor
——————————————————–
so
——————————————————–
so in absense of curvature: , then
——————————————————————————————–
How do a covector field varies along ?






maestro tengo una duda sobre el porque de la existencia del tensor se Riemann, en este articulo: http://es.wikipedia.org/wiki/Tensor_de_curvatura al principio hablan de como el tensor de Riemann describe la curvatura de variedades de cualquier dimensión y que cualquier otra curvatura se obtiene a partir de este, mi pregunta es: por que necesariamente un tensor de rango 4 escribe cualquier curvatura?, por que tiene que ser el tensor de Riemann y no alguna otra entidad matematica, y por que necesariamente ese rango?, hay alguna demostracion?.
gracias de antemano maestro, pasela bien estas vacaciones
David, las preguntas que planteas muy válidas tienen respuestas elaboradas que conviene que tu las re-elabores,,, hay un libro clasiquísimo de Manfredo do Carmo titulado Riemannian Geometry del 1992, en el cuenta la historia de los trabajos de Gauss en superficies y de como Riemann con mucha visión multidimensional dió a Christoffel la inspiración para la formulación que ahora disfrutamos,,, ¿Conoces el libro de Roger Penrose llamado “La nueva mente del emperador” ? en el dice como entender las partes del tensor, en términos del de Weyl y el de Ricci y de como la energia y la materia se alinean en el lenguaje de la curvatura,,, Pero wikipedia en español nomas no te va a sacar de dudas o te puede confundir levemente lo cual es bueno, en el f.english está un poco mejor,,, : )
–
Saludos
gracias profe, y para quien le interese aquí están los links de los libros que él mencionó:
Click to access Riemannian_Geometry.pdf
Click to access Roger.Penrose.-.La.Mente.Nueva.Del.Emperador.pdf
prueba $\sum_{k=0}^{\infty}a_kx^k$ poniendo un latex y un espacio, entre el primer “pesos” y el backslash de “sum”… para obtener:
maestro y que onda con eso de que el nakahara define el map con productos tensoriales en vez de cartesianos?
no conozco el contenido del Nakahara…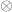 , pero es obvio que
, pero es obvio que  come tres campos vectoriales y arroja uno (tri-linealmente):
come tres campos vectoriales y arroja uno (tri-linealmente):
ni que signifique para él el producto
Por fa, checate la versión
http://de.wikipedia.org/wiki/Riemannscher_Kr%C3%BCmmungstensor
en germano donde dice que la definición considera:
donde es el conjunto de los campos vectoriales en
es el conjunto de los campos vectoriales en  , por cierto, lo mismo que
, por cierto, lo mismo que  …
…
aporto:
si
entonces
Algunos autores suelen escribir para
para  , donde están apareandose un covector (básico) con un contravector (básico)…
, donde están apareandose un covector (básico) con un contravector (básico)…
ha pues si, ahi ya esta explicito, es la propia definicion del map, me faltaba considerar la base del espacio vectorial imagen, gracias maestro
ha que mala onda no se puso bien lo de latex, bueno era algo asi: R : x(M) ⊗ x(M) ⊗ x(M) →x(M)el tensor de curvatura mapea -trilineal:
-trilineal:
donde es el conjunto de los campos vectoriales de
es el conjunto de los campos vectoriales de  …
…
También habría de considerarse que no necesariamente es un espacio euclideano
no necesariamente es un espacio euclideano 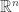 sino más bien como un espacio topológico cualquiera, más específico: una variedad diferenciable (differential manifold), a el cual será medida su curvatura… como el ejemplo de las superficie en
sino más bien como un espacio topológico cualquiera, más específico: una variedad diferenciable (differential manifold), a el cual será medida su curvatura… como el ejemplo de las superficie en 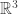 …
…
si maestro, a esa me refiero, hay alguna demostración de por que se define así?, he visto varias demostraciones pero que se refieren directamente a las componentes del tensor (el que sale al evaluar esa formula de arriba evaluada en los vectores básicos producto interior con covector basico)
según entiendo el “extraterrestre” B. Riemann y B. Chrsitoffel lo desarrollaron observando todo el enjambre de curvaturas que disponian en su tiempo (curvatura y torsión de curvas, curvatura gaussiana,…)
por fa checate:
http://en.wikipedia.org/wiki/Riemann_curvature_tensor
y quizás eso te ayude un poco más… la versión en el fregado gachupín no ayuda mucho…
y otra cosa maestro, creo que la base esta incompleta cuando deriva covariantemente al tensor T que tiene en negritas
efectivamente…
cómo ejercicio de latex ¿porqué no escribes la corrección?
corrected: the latex, content: fine, but improved and enhancing
maestro tengo una duda que olvide preguntarle hoy que lo vi, es fácil checar la formula del tensor de curvatura y calcularlo para los distintos casos, pero por que se definió así?, cual es la abstracción o la visión detrás del tensor?, hay alguna demostración?, yo cheque que en parte fue producto de preguntarse si hay alguna importancia en el orden de derivación covariante de las variables, que de hecho lo hay.
te refieres a
maestro en internet y en muchos textos una vez teniendo esa expresión se observa que para obtener las componentes del tensor usual (1,3) se evalúa eso de ahí en vectores basicos y se hace producto interior con un covector basico de la base dual,
no entiendo muy bien este ultimo paso aunque al leer el Nakahara y wikipedia me di una idea,
según entiendo es análogo a una función escalar (tomando en este caso una dependiente de dos variables), en esta evaluamos desde R^2 y nos lanza un escalar, el producto cartesiano nos lanza un punto que vive en R^3, ahora con el tensor de riemann: teniendo la expresion de arriba que veo que le nombran operador de curvatura, tenemos un campo tensorial que el nakahara lo espresa como
entonces asi como la funcion escalar es un punto en R^3 (quiza abusando del lenguaje) entonces el operador de curvatura con el uso del producto tensorial entre su imagen y preimagen nos da un tensor que vive en un correspondiente espacio vectorial cuyas bases sabemos que definen tensores mixtos de rango 4 mixto (1,3)
edité un poco este comentario para que puedas formular un poco mejor tus conceptos y tus preguntas…